四元数与万向锁

最近的学习中关于四元数和万象锁出现的频率比较高，因此认真学习了，做个笔记。

在正式讨论之前，我们需要了解一些基础概念。譬如欧拉角。

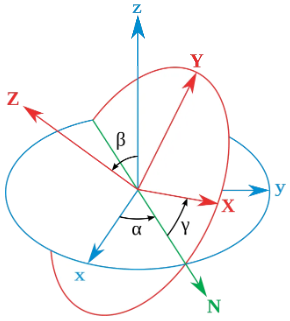
• \alpha (进动角) 是 x - 轴与交点线的夹角
• \beta (章动角) 是 z - 轴与 Z - 轴的夹角
• \gamma (自旋角) 是交点线与 X - 轴的夹角。

简单点来说，就是分别围绕 $xyz$ 轴进行旋转的角度。可以用来描述三维空间中的物体旋转。但是欧拉角又有静态和动态之分。

静态欧拉角，即以固定的参考系（又称实验室参考系）来进行旋转。譬如，我们旋转一个物体，不管一个物体怎么旋转，我们整体的参考系并不会发生变化。

但静态欧拉角对于描述场景中的物体旋转并不方便，譬如一个立方体使用世界坐标系（静态欧拉角）进行旋转后，我们只需要立方体根据其自己 z 轴再进行旋转，静态欧拉角便很难进行描述。

因此我们还需要可以独立描述物体旋转的欧拉角，也就是动态欧拉角。即这时物体的 xyz 轴应该是跟着物体发生变化的。
注意，动态欧拉角的旋转顺序对于物体最终选择是有影响的，所以只有固定的顺序（同时也正是这个顺序导致了后续的万向锁问题）才能确定物体最终的旋转姿态。因为当第一次旋转发生时，它的其余坐标轴位置也发生了改变。

欧拉角旋转，在计算机中通常实现为 Y -> X -> Z。关于 Unity 中的旋转顺序网上资料参差不齐，有人说是 YXZ，也有人说是 ZXY。我们不妨自己打开 Unity 来试一下。

我们先绕 Z 轴（蓝色）旋转 30 度。假设 Unity 的旋转顺序是 ZXY，那么此时我们旋转 X 轴，应该会和我们想象的一样，绕红轴进行旋转。

很明显，立方体并非绕着 X 轴旋转，它最后的姿态，应该是先进行了 X 轴旋转，再对应进行了 Z 轴旋转。
我们再做一次实验。先绕 X 轴旋转 30 度，再旋转 Z 轴。

我们可以看到这次立方体很好地绕着 Z 轴旋转。同理再试验一下与 Y 轴的对比，因此我们可以得到顺序是 YXZ。

万向锁一旦选择 ±90° 作为 pitch 角，就会导致第一次旋转和第三次旋转等价，整个旋转表示系统被限制在只能绕竖直轴旋转，丢失了一个表示维度。

万向锁纯读定义来说，确实有些让人费解。
如果你喜欢从数学上理解，不妨点击此处读一读 krasjet 大佬的数学解释 。而我则从我更直观的感受上进行介绍。做个 1 分钟的物理实验即可。

首先请读者拿出平时最常使用的手机，然后确定手机的物体坐标系朝向，假设 z 轴与手机屏幕垂直（手机平放于桌面）指向上方，手机较短的一条边为 x 轴，较长的一条边为 y 轴（方向由手机尾部指向头部），物体坐标系的原点是手机左下角的顶点。（注意旋转顺序为 zyx）

绕 z 轴旋转任意角度（注意 x 和 y 轴也跟着一起旋转），再绕 y 轴旋转 90°，再绕 x 轴旋转任意角度。通过多次尝试，会发现一个共同点：z 轴永远是水平的， 通俗的说，手机永远也不会立起来（旋转形成的三维空间是固定的）！本来以为手机会指向任何方向，但实际上手机好像是被锁在桌面上，只能指向水平的某个方向，这个现象就称为万向锁。

动态欧拉角必须按顺序旋转特性的一个体现，而万向锁正是一个极端案例。

那么我们如何解决这个问题呢？
这就涉及到了四元数的概念。

四元数

借助视频很容易理解复数和四元数的几何意义，非常值得一看。如果你是一个数学爱好者，文字版的数学公式推导证明在此处。

我学习之后的总结概括如下。

简而言之，我们可以从四元数的几何意义出发去理解。四元数就好比四维世界的数字。

复数

复数的基本形式是 $z=a+bi$，比如 $3.14+1.59i$ 就是一个复数。它有一个虚数单位 $i$，定义是 $i*i = -1$。

我们将其看作普通的平面坐标系，实数部分放置于 x 轴，虚数部分放置于 y 轴。

$i$ 乘以一个复数相当于将其逆时针旋转 90 度，即此时由 $1+0i$ 变到了 $0+1i$ 。继续逆时针旋转 90 度，$0+1i$ 变为了 $-1+0i$，也就是$i*i = -1$。所以复数相乘，就好比做矩阵变化（旋转 + 拉伸）。

同理将其扩展到四元数，便好比在三维空间做变换（旋转 + 拉伸）。

四元数乘法：（这也是我们告诉计算机该如何去计算它）

对于矩阵乘法，四元数乘法更加简洁

$$\begin{array}{c} i^{2}=j^{2}=k^{2}=-1 \\ i j=-j i=k \\ k i=-i k=j \\ j k=-k j=i \end{array}$$

四元数
比如写一个四元数：$3.23 + 8.46i + 2.64j + 3.38k$（ Hamilton 用了一个特殊的词来称呼没有标量部分只有 $i j k$ 分量的四元数，一个之前没有在数学和物理中出现过的词，向量（Vector）。）

对于旋转来说，我们通常使用单位四元数。

单位四元数：$w^2 + x^2 + y^2 + z^2 = 1 \\$
$j = 0 + 0i + 1j + 0k$ 相当于绕 j 轴旋转了 $90^\circ$。
这时，只会对变换的向量进行旋转，而不会改变其本身的大小。（模长）
$(w_0+x_0i+y_0j+z_0k)(x_1i+y_1j+z_1k)(w_0-x_0i-y_0j-z_0k)\\$
作用：避免了欧拉角的歧义问题。

• 优点：四元数旋转不受万向锁的影响。
• 局限性：单个四元数不能表示任何方向超过 180 度的旋转。
• 局限性：四元数的数字表示在直观上难以理解。

我想从更加直观地感受上来描述一下，我们为什么使用四元数？
回顾一下，正如上文所说，单位四元数可以起到的作用是对三维空间物体进行旋转。

而我们想要描述物体旋转，对于用户来说，欧拉角是最直观的方式。

对于游戏引擎等来说，我们通常有一个世界坐标系，同时也希望子物体也有自己的坐标系，以便我们单独旋转子物体。这时我们不得不使用动态欧拉角。

但是动态欧拉角有缺陷，因为它必须依照固定旋转顺序（如 YXZ），才能真正确定一个旋转。因此各种仿真模拟软件通常会有其自己的固定顺序，即便用户用不同的顺序去设置 XYZ，最后也根据软件自己实现的顺序来展示物体的旋转。
这样才能保证 XYZ 值，只确定一个旋转。

因为旋转顺序固定，所以产生了万向锁。
因此我们需要一个东西它可以唯一确定并表达旋转，于是我们用到了四元数。
但对于用户来说，旋转场景中的物体要自己计算设置四元数显然是不友好的，因此 Unity 等方案都是在内部存储为四元数，而为了用户方便操作理解，UI 面板上则仍然使用欧拉角表示旋转（因此我们可以在软件里复现万向锁的表现），但我们只要自己知道旋转顺序，就可以在设置的时候避开它，设置出自己想要的旋转。