继RWKV、Mamba、KAN之后号称超越Transformer的线性架构TTT又来了

论文

发布日期: 2024-07-20

更新日期: 2024-07-23

文章字数: 2.3k

阅读时长: 8 分

继RWKV、Mamba、KAN之后号称超越Transformer的线性架构TTT又来了

最早从 23 年 5 月的RWKV(RKWV 系列从 V1 更新到 V6，并且作者确实认真做了不少事情的)，再到去年 12 月的Mamba，到今年 4 月的KAN，再到 5 月的Mamba2，到现在的TTT。
What KAN I say？Mamba out！T_T

先简单回顾一下

RWKV: Reinventing RNNs for the Transformer Era

RWKV（Receptance Weighted Key Value）模型的架构，和 Transformer 非常类似，也是由多个 RWKV block 组成，最后加一个 language modeling head 输出下一个 token 的分布概率。每个 RWKV block 内部，有一个 Channel Mix 和一个Time Mix 模块。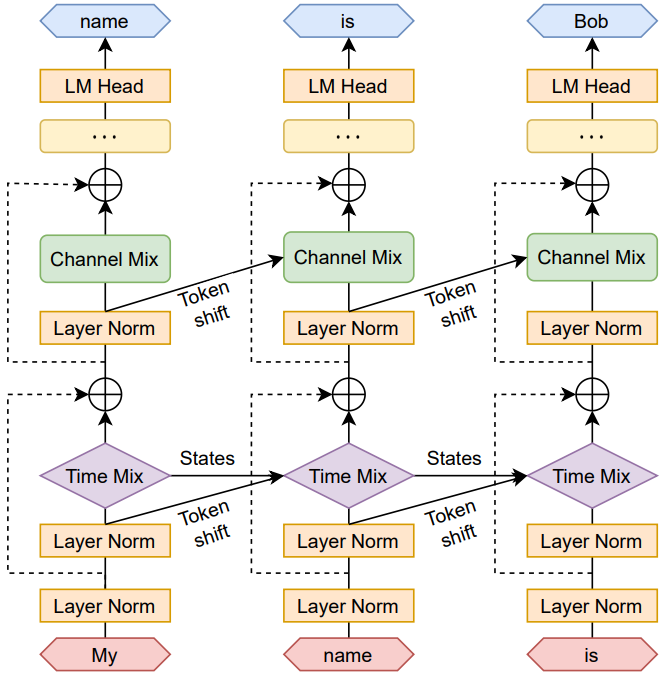语言建模的RWKV架构

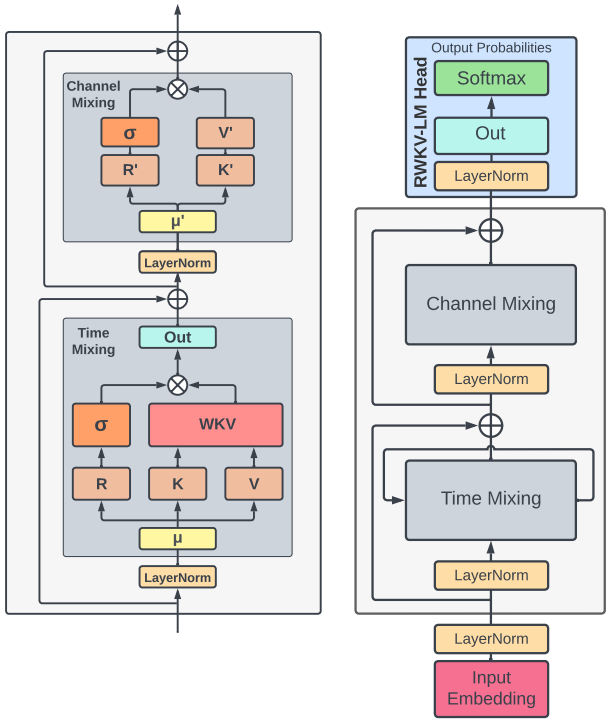RWKV block 内部的 Time Mixing 和 Channel Mixing 模块： RWKV块内的元素（左）和完整的RWKV残差块，配备有用于语言建模的最终头（右）

首先看Time-Mixing Block。Time-Mixing的目的是“Global Interaction”，对应于Transformer中的Self-Attention。

R 表示过去的信息，用 Sigmoid 激活，遗忘机制。
W 和相对位置有关， U 对当前位置信号的补偿。
WKV 类似 Attention 功能，对位置 t ，表达了过去可学习的加权和。

其中使用到的 R、K、V 对应于 Transformer 中的 Q、K、V。也就是说，K、V 的含义可以强行看作一致，把 R 当做 Q 来处理就行。只是 RKV 的计算方法有点变化：
$\begin{matrix} r_{t} = W_{r} \cdot (μ_{r} ⊙ x_{t} + (1 - μ_{r}) ⊙ x_{t - 1}), (11) \\ k_{t} = W_{k} \cdot (μ_{k} ⊙ x_{t} + (1 - μ_{k}) ⊙ x_{t - 1}), (12) \\ v_{t} = W_{v} \cdot (μ_{v} ⊙ x_{t} + (1 - μ_{v}) ⊙ x_{t - 1}), (13) \end{matrix}$

首先，输入经过 LayerNorm 后，将当前位置和前一个位置的输入按权重做一个 Mix，然后分别投影成 R, K, V (公式 11,12,13)。可以看到，这里就是在投影前把历史信息 Mix 起来了，越久的历史，其权重就越小（衰减速率由 μ 控制）。R 通过非线性函数 Sigmoid，得到的结果叫 Receptance，我的理解有点类似于 RNN 里的 Forget Gate 。

然后是最重要的 Attention 用了如下方法计算：
$w k v_{t} = \frac{\sum_{i = 1}^{t - 1} e^{- (t - 1 - i) w + k_{i}} ⊙ v_{i} + e^{u + k_{t}} ⊙ v_{t}}{\sum_{i = 1}^{t - 1} e^{- (t - 1 - i) w + k_{i}} + e^{u + k_{t}}} . (14)$
WKV 这块（公式 14）是 Time Mix 的核心，它的作用就是前面提到的 RWKV 的 "注意力" 机制。 WKV 的计算有点类似于 Softmax，但是在分子和分母上分别加了一个当前位置 $V_t$ 的项。和注意力公式差不多， $WKV_t$ 可以理解为：位置 t 相对于它之前各个位置的相关性（注意力程度）， $WKV_t$ 是一个大小为 C 的向量（C 是 channel 数）。R、K、V 的计算和 Transformer 的区别是，作为计算 RKV（QKV）的输入的 x 不再是当前 token 的 Embedding，而是当前 token 与上一个 token embedding 的加权和。

最后， Receptance 和 WKV_t 相乘（Element-Wise Product，两边都是大小为 C 的向量），得到位置 t 的输出 ot （也是大小为 C 的向量）。显然， $o_t$ 的计算包含了历史信息，随着 t 的增加， $o_t$ 会依赖于越来越长的历史。

RWKV 的优点：结合了 Transformer 和 RNN 的优势，训练时能够像 Transformer 那样并行计算，推理时又能像 RNN 那样高效。尤其是后者，对于降低模型成本，尤其是在端侧部署有重要意义。另外 RWKV 的计算量与上下文长度无关，对于更长的上下文可能有更好的扩展性。
RWKV 的缺点：和 RNN 一样，历史信息是靠隐状态（WKV）来记忆的，对于长距离历史信息的记忆不如 Transformer。这个很容易理解，因为 RWKV 的历史信息是存在一个向量里，时间越久衰减就越厉害，与 Full Attention 比自然是有局限性的。这个局限性也使得 Prompt Engineering 对 RWVK 更加重要。与 Transformer 相比，由于 RWKV 对很长的上下文记忆能力有限，如何设计提示对模型的性能会有很大影响。

Mamba: Linear-Time Sequence Modeling with Selective State Spaces

Mamba 的架构主要基于 S4 (Structured State Spaces for Sequence Modeling)，这是一种最新的状态空间模型 (SSM，State Space Model) 架构。详细介绍
可见一文通透想颠覆 Transformer 的 Mamba：从 SSM、HiPPO、S4 到 Mamba，内容非常详细全面，这里不再赘叙，同时也推荐一下作者七月。

Mamba 优点：

改进 transformer 不擅长处理超长的序列的问题，随上下文长度的增加实现线性扩展。
快速训练和推理。在训练过程中，计算量和内存与序列长度成线性关系，而在推理过程中，由于不需要缓存以前的元素，自回归展开模型每一步只需要恒定的时间。

Mamba 缺点：

结构化 SSM 最初被定义为连续系统的离散化版本，对于连续时间数据（如音频、视频）具有较强的归纳偏差。
选择机制克服了结构化 SSM 在文本和 DNA 等离散数据模态上的弱点，但反过来可能会影响它们在 LTI (线性时不变) SSM 擅长的数据上的性能。
基于 Transformer 的基础模型（特别是 LLMs）具有丰富的性质和与预训练模型交互的模式，如微调、适应性、提示、上下文学习等，Mamba 可能不具有相似性质。
实证评估局限于小型模型规模，在大多数强大的开源 LLMs（如 Llama）以及其他循环模型（如 RWKV 和 RetNet）的阈值以下。评估 Mamba 在这些较大规模上是否仍然有利尚待评估。

KAN: Kolmogorov-Arnold Networks

KAN 网络结构思路来自 Kolmogorov-Arnold 表示定理。MLP 在节点（“神经元”）上具有固定的激活函数，而 KAN 在边（“权重”）上具有可学习的激活函数。在数据拟合和 PDE 求解中，较小的 KAN 可以比较大的 MLP 获得更好的准确性。

KAN 本质上是样条（Spline）曲线和 MLP 的组合，吸收了两者的优点。即KAN = MLP + Spline（在数学中，样条曲线是由多项式分段定义的函数。一般的 Spline 可以是特定区间的 3 阶多项式。在插值问题中，样条插值通常优于多项式插值。）

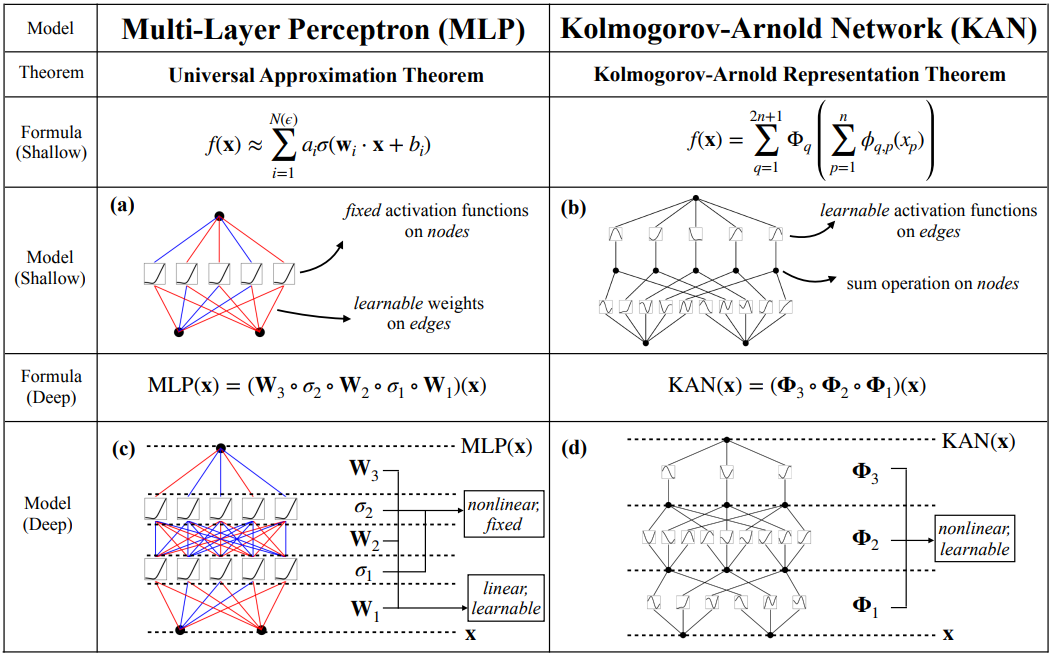
与传统的 MLP 相比，KAN 有 4 个主要特点：

激活函数位于 "边" 而不是节点（Node）上。
激活函数是可学习的而不是固定的。
可以使用非线性核函数来替代 MLP"边"（Edge）上的线性函数。
可以设定细粒度的结点（Knot）来提高逼近精度。

KAN 优点：

使用非线性算子（典型的是样条）可以更快的逼近任意函数。
精度高

KAN 缺点：

训练代价大，训练速度慢（KAN 通常比 MLP 慢 10 倍）。

此处使用 MNIST 数据集测试 MLP 和 KAN，感兴趣的小伙伴可以试一下 (亲测可用)

TTT：Learning to (Learn at Test Time): RNNs with Expressive Hidden States

TTT 层作为一种新的信息压缩和模型记忆机制，可以简单地直接替代 Transformer 中的自注意力层。关键思想是使隐藏状态本身成为机器学习模型，而更新规则则成为自监督学习的步骤。通俗来说，在以前，习惯的做法是把某个函数的输出当作Hidden State，通常是一个向量（如RNN）或者很多向量（如Transformer）。但TTT把自己(模型)当作了Hidden State。而这个hidden state的更新是靠一次基于反向传播的更新。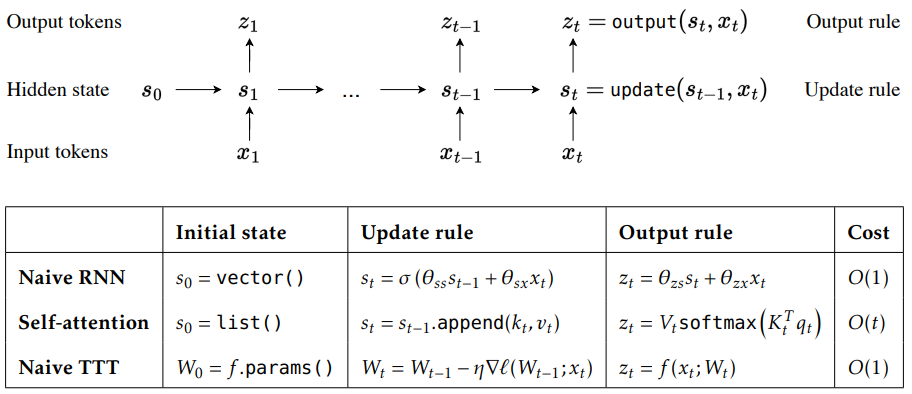 RNN、注意力、TTT对比

序列模型会把历史上下文存储在一个隐藏状态中，这是不可避免的。像Mamba这样的RNN层，会随着时间的推移压缩成一个固定大小的状态，它们虽然效率很高，但性能受限于其表达能力。对于Transformer中的注意力机制，其有一个KV缓存，它会随着时间的推移不断增长。这个状态不会压缩任何历史上下文，但随着上下文长度的增加，成本也会越来越高。因此，TTT架构另辟蹊径，把上下文压缩到模型的权重中。与 Transformer 的Hidden State不同（每读一个token，就完整地扫描整个历史进行查找），TTT 不会随着处理数据的增多而无限扩展。相反，它会将数据编码成一组代表性的变量，即"权重"。这种形式是 TTT 模型高性能的原因，无论 TTT 模型处理多少数据，其内部模型的大小都不会改变。

TTT 优点：

高效率。

TTT 缺点：

TTT 架构的验证案例相对较少，主要集中在特定任务和小规模实验中，尚未在大规模实际应用中得到广泛验证。

最后，我想说 TTT 的本质依然是 RNN，并且从算法的角度看，这种用空间复杂度（这种说法其实不恰当）置换时间复杂度（长上下文查找效率）的方式导致的结果就是表达能力差，直观的理解就是对于几万的 token 使用的模型参数假设是 1MB，但这 1MB 参数真的能表达几万亿的 token 内容吗，这也是作者只在 1.2B 参数内进行实验的原因吧。

总结：喜大普奔，大家又可以水论文了！T_T

liuli

https://liuliai.github.io/2024/07/20/Learning%20to%20(Learn%20at%20Test%20Time)%20RNNs%20with%20Expressive%20Hidden%20States/